斐波那契Fibonacci，两种方法

斐波那契：

$$ F(n)=\begin{cases} 0, n=0\\ 1, n=1,2\\ F(n-1)+F(n-2), n>2\\ \end{cases} $$

方法一

function Fibonacci(n) {
    if (n === 0) return 0;
    if (n === 1) return 1;
    return Fibonacci(n - 1) + Fibonacci(n - 2);
}

利用上面递推式，自顶向下进行求解，因为存在大量的重叠子问题，时间复杂度为 O($2^n$)。

方法二

我们可以将递推式的求解从自顶向下改为自底向上（循环实现）。简而言之，我们已知前两项的值，然后我们就可以用前两项的值求出第3项的值，接着求第4、第5、……，直到求出第n项的值。

实际上这种方法叫动态规划，一种将复杂问题分解成更小的子问题来解决的优化算法。
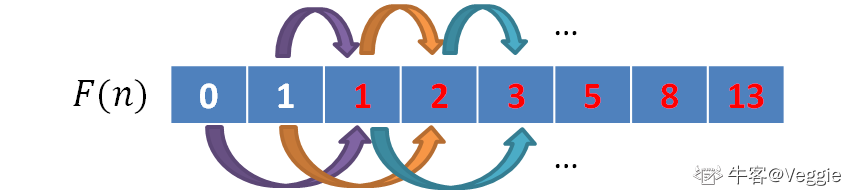
实现过程如下图所示，两个相同颜色的箭头可以确定一个新的数列项。

function Fibonacci(n) {
    if (n === 0) {
        return 0;
    }
    if (n === 1) {
        return 1;
    }
    let a = 0,
        b = 1;
    for (let i = 2; i < n; ++i) {
        let c = a + b;
        a = b;
        b = c;
    }
    return a + b;
}

上述算法的时间复杂度为 O(n)